覆面算を解くテクニック集 - カナンの数学ノート

前回の記事では、$SEND+MORE=MONEY$の問題を例に覆面算の基本的な解き方を紹介しました。

canaan1008.hatenablog.com

今回の記事では、覆面算がさらに解きやすくなるテクニックを5つ紹介しようと思います。

上下入れ替え
同文字消去
繰り上がり分割
恒等式の除去
分岐の少ない道から

(ネーミングは全てオリジナルなので他のところでは通じません。たぶん。)

やっていることは数学的には当たり前のことばかりですが、覆面算を解く上では視覚的な情報量が減るという大きなメリットがあります。

※注意※

この記事内で扱っている覆面算の例はテクニックを紹介するために作成したものであり、解を持たない可能性があります。
各行の最上位の桁は$0$にはなりませんが、変形を行ったあとも必ずしもそうなるとは限りません。
例えば、$SEND+MORE=MONEY$においては$S$と$M$は$0$ではありませんが、テクニックを使って$END$という行が出てきたとしても、$E$が$0$でないとは限りません($E=0$である可能性もあります)。
テクニックを使うと、まだどの文字とも対応がついていない数字が現れる場合があります。混乱防止のため、文字と数字の対応表は必ず書きましょう。
例えば$ABC+DEF=GBH$にテクニックを使うと$A$$0$$C+DEF=G$$0$$H$となりますが、これは何かの文字が$0$と対応づいた、というわけではありません。ましてや$B=0$とも限りません。

上下入れ替え

線より上(足している数)において、同じ桁にある文字や数字を上下に入れ替えることができます。

例えば、こんな時に使えます。

ある程度解き進めたあと、数字だけ、文字だけの行になるように入れ替える
同じ文字が散らばっているとき、それらが同じ行に並ぶように入れ替える
現れた$0$をできるだけまとめることで、桁数の少ない数字を作る

こういう時に使おう！と一概には言えませんが、自分の見やすい形に変形させることができます。

同文字消去

ある桁に着目し、線の上下に同じ文字があったとします。このとき、その文字を取り除いて0に置き換えることができます。

主に問題の解き初めに使うことができるテクニックです。同じ文字を見つけたらサササッと$0$に書き換えましょう。
ただし、先述のとおり置き換えた文字が$0$に対応するわけではないことに注意です。上下から$B$を取り除いただけであり、$B=0$と決まったわけではありません*1。

ただし、同じ文字が線の上に２個以上あった場合はそのうちどちらかのみが$0$になります。

さらにこの例に「上下入れ替え」のテクニックを使う($T$と$0$を入れ替える)ことで、一番上の行を$RUE$にして桁数を減らすことができます。やったね！

また、文字に影響を与えなければ、線の上下に同じ数を足したり引いたりできます。

繰り上がり分割

繰り上がりの量が確定している桁がある場合、その桁で筆算を分割することができます。
分割した右側の筆算では繰り上がりをそのまま答えに下ろし、左側の筆算では足している数に追記します。

個人的に最強のテクニックです。
繰り上がりのメモはどうしても煩雑になりがちです。しかし、このテクニックを使うことで「あ、そうかこの桁は繰り上がりがあるから…」のようにいちいち考える必要が無くなります。
筆算の数が増えてややこしくなったように感じますが、「それぞれの桁数が少なくなる」ことと「繰り上がりについて考える手間が省ける」のはかなりのメリットです。さらに、嬉しいことに恒等式が生まれてくる可能性もあります。恒等式については後述します。

また、当たり前ですが繰り上がりが起こらないとき(繰り上がりが$0$のとき)はそのまま分割できます。

恒等式の除去

分割した筆算が恒等式(文字にどの数字を当てはめても成り立つ式)の場合、その筆算は消去することができます。

また、これは文字に限らず数字だけの式( $4+6=10$ など)が筆算の形で出てきても同じように消去できます。
恒等式は覆面算を解く上で何の情報も持たないのです…

分岐の少ない道から

いいネーミングが思いつきませんでした。誰か考えて。

これは数学的なテクニックではなく、場合分けで効率良く解くテクニックです。

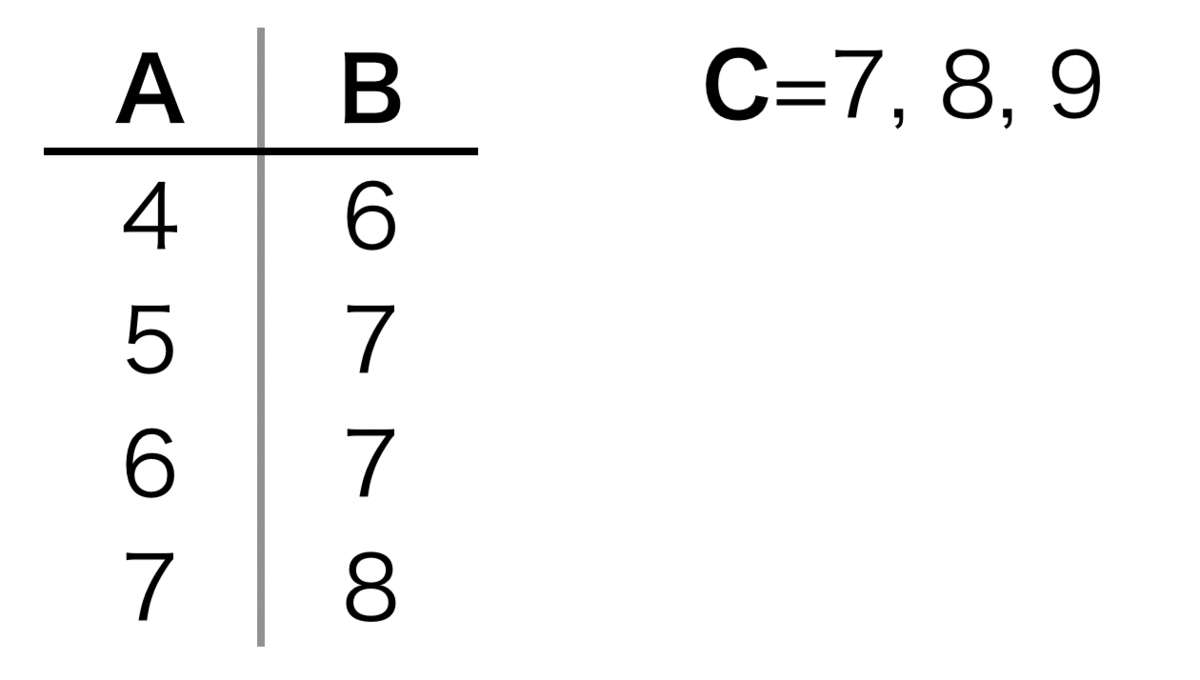
例えば、$A, B$に表のような関係があったとし、$C$は$7, 8, 9$のいずれかであることがわかっているとしましょう。

さて、あなたは解き進める手が止まったため、$C$の値で場合分けをして正解を探すことにしました。
このとき、最初に進むルートはどの$C$の値が良いのでしょうか？

実際の覆面算の状態にもよりますが、ここではまず$C=7$を選ぶのが一番スマートのように感じられます。
なぜならば$C=7$と仮定すると$A, B$の組み合わせは自ずと一つに定まりますが、$C=8, 9$の道を選んだ場合は$A, B$の組み合わせの選択肢が3つ、4つとありその後の場合分けがさらに大変になるためです。

つまり場合分けでは、他の道をできるだけ多く潰せる道から進めということです。

しかし、結局その道が正解とは限らないんでしょ？と思うかもしれません。
そのとおりです。その道が正解とは限りません。
ですが、この方法には下記に示す2つの大きなメリットがあります。

正解だった場合、いち早く正解にたどり着けます。
一度に多くの道を潰せるため、次の場合分けが少なくなり正解にたどり着きやすくなります。
間違いだった場合、いち早く間違いだと気づいて戻れます。
上記の例の場合、$C=7$と仮定してそれが間違いであることは場合分けなしで知ることができます。一方、$C=9$と仮定してそれが間違いであることは$A, B$の組み合わせを４パターン試さないと知ることができません。

迷路を進むときに分岐路にさしあたり、それぞれの方向を示す看板に"その後の分岐路の個数"が書いてあったら、その数字が少ないほうから進むでしょう？
たとえその方向が間違いだったとしても、すぐに間違いだと気づけるかもしれないんですから。