トーナメントの数え上げ
この記事は前回の記事の続編…にしようと思ったのですが、予備知識について書いていたら1.5記事ぶんくらいになったので単体の記事にしました。
canaan1008.hatenablog.com
今後の方針としては、↑の記事で扱ったような多義文の解釈の数え上げについて触れる予定です。
要するに、可連結かどうかの制限付きなトーナメントの数え上げをしたいわけです。
ですが、この数え上げをするにはそもそも可連結かどうかの制限がないトーナメントの数え上げについて理解する必要がありました。そりゃそうだよね
ということで、一旦多義文のことは忘れてトーナメントの数え上げについて考えていきます。
簡単な例から数えてみよう!
先に断っておきますが、本記事でのトーナメントとは「出場者が上に並び、試合が進むほど下に移動していく」ようなトーナメントとします。別にどっちでもいいんですが、多義文について考えすぎた結果こっちが自然なトーナメントに見えてきてしまったので。
また、出場者は区別しません。あくまでもトーナメント表の"形"のみに着目します。
1人トーナメント
それでは問題です。
出場して、そのまま真っすぐ優勝まで進めるので、下図のようなトーナメント表のみです。答えは1通りです。

図を作っていていたたまれない気持ちになってきました。
2人トーナメント
次の問題です。
2人が対決して勝ったほうが優勝して終わり。よって下図のようなトーナメント表のみで、答えは1通りです。
わかりやすくするとこんな感じです。

何当たり前のことを書いてるの?と思うでしょうが、これが後から効いてくるんですよ。
3人トーナメント
どんどん行きます。
3人のうち左の2人がまず対決するか、右の2人がまず対決するかでトーナメント表が変わります。
答えは、2通りです。

これもわかりやすくするとこんな感じです。

ここで注目してほしいのは、決勝の両側にいる人数です。
左のトーナメントでは決勝の左に1人、決勝の右に2人がスタンバイしているのに対し、
右のトーナメントでは決勝の左に2人、決勝の右に1人がスタンバイしています。
ふむふむ、まあ言われてみればそうだよね、と。
これまでの答えをまとめるとこうなります。
| 人数 | トーナメントの数 |
|---|---|
1 |
1 |
2 |
1 |
3 |
2 |
このまま表に書いていってもいいんですが、せっかくなので数学っぽく書きましょう。
1人トーナメントの数を、2人トーナメントの数を
、3人トーナメントの数を
と書きましょう、ということを言っているだけです。
先ほどの表を数式を使って書くと、\begin{eqnarray}
T_1&=&1\\
T_2&=&1\\
T_3&=&2
\end{eqnarray}です。
いや別にわざわざって書かなくてもいいじゃんって思うかもしれませんが、こうすることで例えば「1人トーナメントと3人トーナメントの合計の和」と言いたいときに
と書くだけで済みます。これが†数式の力†です。強いね。
ちなみにはトーナメント(Tournament)の
です。何でも良かったんだけどね。
4人トーナメント
ここからじわじわとカタラン数みが出てきます。準備はいいですか?
もし余裕があれば何か紙に書きながら自分で考えてみるとよいでしょう。
(言い換え:
よろしいですか?
それでは答え合わせです。
4人トーナメントは、下図のように5通りです。つまり、です。

これも決勝の両側の人数を見てみましょう。

この図をよ〜く見てみると、あることに気づきます。たとえば左の2つ。
……あっ!!!

ここの2つ、3人トーナメントに出てきた2パターンそのものじゃん!
そうです。決勝の右側に3人いる場合、その中で3人トーナメントが行われていますね。
この話は3人に限った話ではありません。
決勝の両側が1人/2人/3人すべての場合において、それぞれの人数におけるトーナメントが出現していることがわかります。
(オレンジ枠は全て1人トーナメント、青枠は全て2人トーナメント、緑枠は全て3人トーナメント)
ではそろそろもったいぶるのをやめて、トーナメントの数え方について説明します。
今後の説明を簡単にするために、決勝の左側にあるトーナメントを左予選、決勝の右側にあるトーナメントを右予選と呼ぶことにします。
左予選と右予選での優勝者が決勝でぶつかり合い、チャンピオンが決まるってことですね。
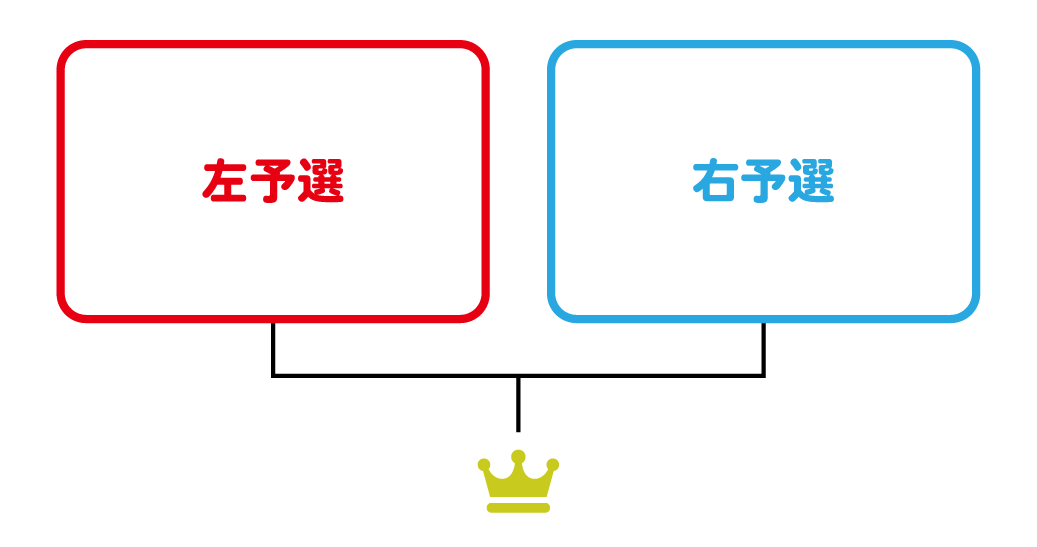
4人トーナメントは、次のような3つのパターンに分けられます。
- 左予選が1人、右予選が3人
- 左予選が2人、右予選が2人
- 左予選が3人、右予選が1人
4人をどのように両側の予選に振り分けるかを考えるので、この3つのパターンになるのは納得いくかと思います。
そしてここが重要なポイント。
それぞれの予選では、その人数に応じたトーナメントを全パターン行うことができます。

例えば、左予選が1人/右予選が3人の場合。
左予選の参加者は1人なので、1人トーナメントが作られます。これは通り。
右予選の参加者は3人なので、3人トーナメントが作られます。これは通り。
左予選と右予選がどのように行われるかはお互い影響を与えないので、左予選が1人/右予選が3人のトーナメントは通りあります(掛け算の記号は省略しています)。
同様に考えて、
左予選が2人/右予選が2人の場合は通り。
左予選が3人/右予選が1人の場合は通り。
のトーナメントを作ることができます。

最終的に知りたい4人トーナメントの数はこれら全ての和ですので、\begin{eqnarray}
T_4&=&T_1T_3 + T_2T_2 + T_3T_1\\
&=& 1 \cdot 2 + 1 \cdot 1 + 2 \cdot 1 \\
&=& 2 + 1 + 2\\
&=& 5
\end{eqnarray}となり、めでたく、つまり4人トーナメントが5通りであることがわかりました。
5人トーナメント
では次の問題です。
(言い換え:
まずは、5人が出場するときの左予選と右予選の内訳を考えてみます。
- 左予選が1人、右予選が4人
- 左予選が2人、右予選が3人
- 左予選が3人、右予選が2人
- 左予選が4人、右予選が1人
そして先ほどと同じように、それぞれの予選でその人数のトーナメントを作ることができますね。

左予選が1人、右予選が4人となるトーナメントでは、左予選のトーナメントが通り、右予選のトーナメントが
通りあるので、これらをかけて
通りあります。
同じように考えると、残りのパターンは通り、
通り、
通りあるので、これらを全て足せばよいわけです。\begin{eqnarray}
T_5&=&T_1T_4 + T_2T_3 + T_3T_2 + T_4T_1\\
&=&1 \cdot 5 + 1 \cdot 2 + 2 \cdot 1 + 5 \cdot 1\\
&=& 5+2+2+5\\
&=& 14
\end{eqnarray}となるので、、つまり5人トーナメントは14通りあることがわかりました。
ですが、今回はこれまでと違った方法で求めましたね。実際に全パターンを書くことなく数え上げることができたんです。
両側の予選の人数の割り振りを考えることで、1人〜4人トーナメントの総数から、5人トーナメントの総数を求めることができました。
数式を使って言うならば、を使って
を計算することができたんですね。
では、これまでの情報(1人〜5人トーナメントの総数)()から6人トーナメントの総数(
)も数え上げることができるのでは????
6人トーナメント
(言い換え:
- 左予選5人/右予選1人のとき、
通り
- 左予選4人/右予選2人のとき、
通り
- 左予選3人/右予選3人のとき、
通り
- 左予選2人/右予選4人のとき、
通り
- 左予選1人/右予選5人のとき、
通り
これらを全て足せばよいので、\begin{eqnarray}
T_6&=&T_5T_1 + T_4T_2 + T_3T_3 + T_2T_4 + T_1T_5\\
&=&14 \cdot 1 + 5 \cdot 1 + 2 \cdot 2 + 1 \cdot 5 + 1 \cdot 14\\
&=& 14 + 5 + 4 + 5 + 14\\
&=& 42
\end{eqnarray}です。よって、、6人トーナメントは42通りです。一気に増えたな!
図も無しで話を進めてしまいましたが、ここまで読めてこれたならやっていることはわかったのではないかと思います。
それではそろそろ、アレいきましょうか。
 人トーナメント
人トーナメント
一般化です。数学者はす〜〜〜〜〜ぐ一般化したがる。
(言い換え:
左予選が人のとき、右予選は何人でしょうか?全員で
人いるので…右予選はその
人以外、すなわち
人ですね。
左予選が人のときはどうでしょうか?右予選はその
人以外ですので、
人です。
同様に左予選が人のとき、右予選は
人です。
先ほどのように書くと…
- 左予選
人/右予選
人
- 左予選
人/右予選
人
- 左予選
人/右予選
人
- 左予選
人/右予選
人
- 左予選
人/右予選
人
左予選の人数がどんどん増えていって、右予選の人数がどんどん減っていっています。
これは右予選の人数がと減っていって、最終的に
人になるまで続きます。このときは逆に左予選は
人になりますね。(全体が
人なのは変わらないので。)
- 左予選
人/右予選
人
- 左予選
人/右予選
人
- 左予選
人/右予選
人
では、それぞれのトーナメント数を使って、を求めちゃいましょう。
- 左予選
人/右予選
人のとき、
通り
- 左予選
人/右予選
人のとき、
通り
- 左予選
人/右予選
人のとき、
通り
- 左予選
人/右予選
人のとき、
通り
- 左予選
人/右予選
人のとき、
通り
- 左予選
人/右予選
人のとき、
通り
なので、\begin{eqnarray}
T_n&=&T_1T_{n-1} + T_2T_{n-2} + T_3T_{n-3} + \cdots + T_{n-3}T_3 + T_{n-2}T_2 + T_{n-1}T_1
\end{eqnarray}です。人トーナメントの総数(
)が具体的にわからないためバシッと1つの値は求まりませんが、このような式で
人トーナメントの総数を求めることができますね。
再三言いますが、やっていることはこれまでと変わらないです。
- 全体の人数を左予選と右予選にどのように分けるかで場合分けする
- それぞれの分け方で、左予選と右予選のトーナメントの総数がわかるのでその2つを掛け算する
- それぞれの分け方に対してトーナメントの総数が求まったので、最後にそれらを全部足す
ですね。
これまで見てきたように、2人以上のトーナメントを数え上げるときはその人数より少ない人数のトーナメントの総数を知っておく必要があります。
なので、
で、
は
を使って計算できて、
は
と
を使って計算できて、
は
と
と
を使って計算できて、
となりますね。
まとめ
だいぶ長くなってしまいましたが、これで好きな人数のトーナメント表の総数を求める方法がわかりましたね。
ポイントは「両側の予選の人数で場合分けして」「それぞれの予選トーナメントの数をかけて」「それらを足す」ことでした。
実はこのプロセスが多義文を数え上げるにあたって非常に大事になってくるのです。これはまたその時の記事で書くことにしましょう。
それでは。
余談
前回の記事でちらっと話を出しましたが、この数はカタラン数というものです。カタラン数は\begin{eqnarray}
c_0 &=& 1,\\
c_n &=& \sum_{k=0}^{n} c_k c_{n-k}\ \ (n \geqq 1)\\
&=& c_0c_n + c_1c_{n-1} + \cdots +c_{n-1}c_1+c_nc_0
\end{eqnarray}で定義される数列です。ほら、ちょっと似てる!
ちょっと似てる(ちょっと違う)のは、添字が1つズレているからですね。
カタラン数は、試合数が
のときのトーナメント表の総数を表しています。なので、総人数を
としていたときと1つズレてしまうんですね。
実はカタラン数
c_n &=& \cfrac{1}{n+1} \left( \begin{array}{c} 2n \\ n \end{array} \right)\\
&=& \cfrac{(2n)!}{(n+1)!n!}
\end{eqnarray}
一般項の求め方は母関数をマクローリン展開でゴニョゴニョする方法や、対角線を跨がない最短経路問題を頑張って解くことでわかりますが、それこそ1記事書けてしまうので今回は割愛します。というか多義文について考えるときは一般項使わなかったしな!