気まずいトーナメントの数え上げ
この記事は前々回の記事の続編です。
canaan1008.hatenablog.com
また、トーナメント表の数え上げ方法をもとに話が進むので、前回の記事を読んでいない方は是非そちらもお読みください。
canaan1008.hatenablog.com
簡単なあらすじ。
「頭が赤い魚を食べた猫」という文章は、文節同士がどうかかり合うかによって5種類の解釈があります。文節同士の全ての組み合わせが可連結かどうか(その2つの文節を繋げて意味が通るかどうか)に着目してトーナメントを作り上げ、無事にトーナメントを作ることができたら意味が通る、という話を行いました。

この記事では、「それぞれの文節同士が可連結かどうか」から「その文章の解釈の総数」を求めることを目標にします。
みなさんも、普段の生活で多義文を見かけることがあると思います。これから書く方法を身につければ、そのような文章を見かけたときに「この文章は○通りの解釈ができてしまうのでよくありませんね」とドヤ顔で言うことができます。たのしみですね
ちなみにこのあと例え話に移っていきますが、今回は多義文の話に戻ってきません。ゆるしてね
次の記事でその点は書きたい。
気まずいトーナメント
といってもいきなり文節が〜とか可連結で〜とか言ってもわけわからないと思いますので、次のような大会を考えます。別に種目は何でもいいです。じゃんけんでも50m走でもスマブラ(2ストアイテムなし終点7分)でも、みなさんにとって馴染み深い1on1の試合を考えてもらえれば大丈夫です。
- 一郎、二郎、三郎、…、七郎の7人の出場者がトーナメントで戦う。
- 各試合は2人で戦う。
- トーナメントの左端が一郎、右端が七郎になるように順番に対応付ける。

- この7人は一郎が最も弱く、二郎、三郎、…、七郎の順に強くなる。
言いかえ:のとき、
郎より
郎のほうが強い。
よって、一郎は初戦敗北が確定しており、七郎が優勝する。 - この7人のうちの異なる2人について、その2人の関係は「仲が良い」または「仲が悪い」のどちらかであり、仲が悪い2人は対戦することができない。この関係性は大会前に確定しており、公表されている。
顔も見たくないほど仲が悪いので、試合放棄してしまい大会を続行することが不可能になる。 - どの出場者も、自分より強い出場者で仲が良い人が少なくとも一人いる。
例:三郎は、四郎〜七郎で仲が良い人が少なくとも一人いる。(四郎〜七郎全員と仲が悪い、ということはない)
このとき、無事に最後まで大会を遂行することができるトーナメント表は何通りあるか。
自分と仲が良いフォロワー同士がお互いブロックしあっているような、そんな気まずさを感じます。
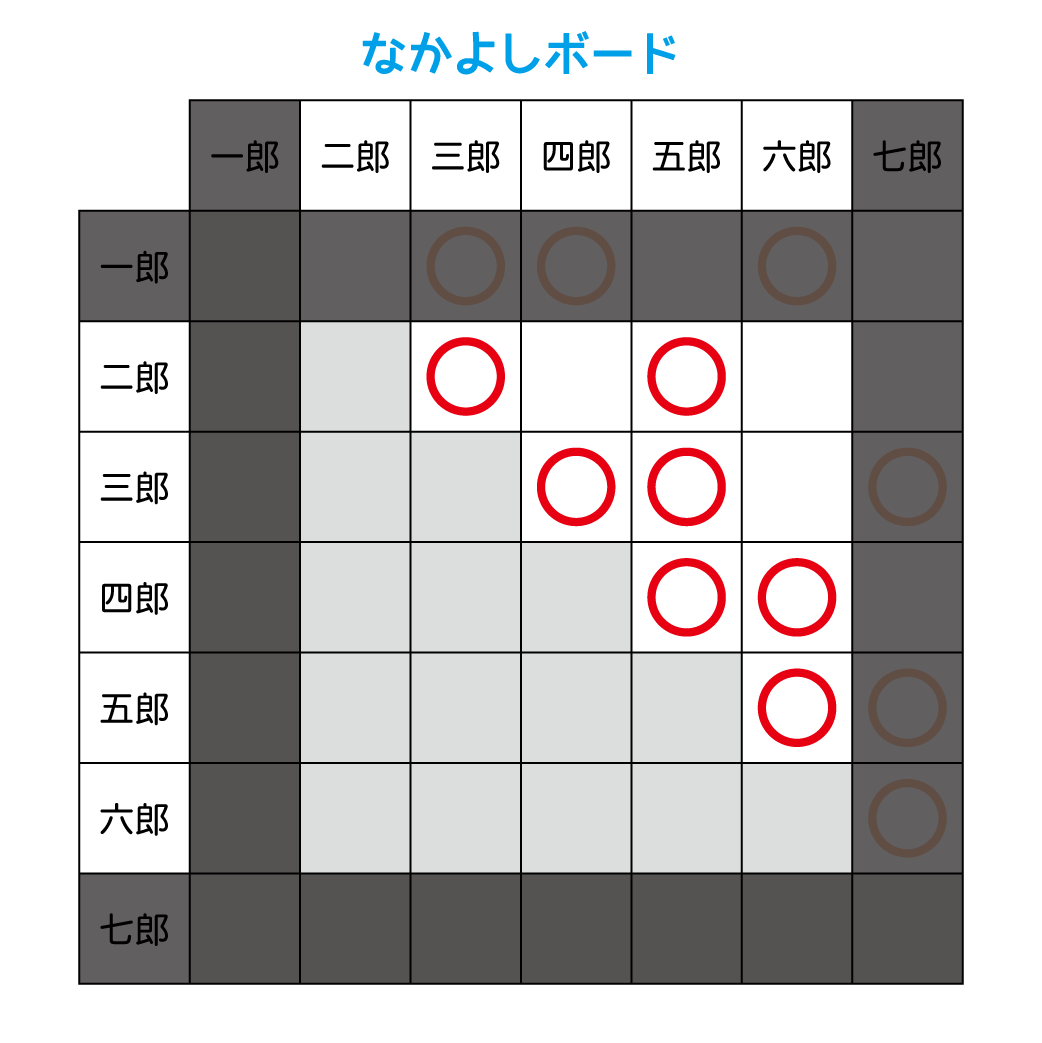
なかよしボード
それぞれの出場者の仲の良し悪しは、1つの表にまとめることができます。そうですね、ほのぼのさせるためになかよしボードとでも名付けておきましょうか。
今回は、なかよしボードが下記のようになっているとして話を進めます。○がついている2人は仲が良く、ついていない2人は仲が悪い、ということです。

名前のほのぼの感が逆効果なのかわかりませんが、仲の良し悪しがこうも浮き彫りになって出てくると一触触発な感じが見えてきてビクビクしますね。飲み会の幹事の方はもしかしていつもなかよしボードを作成していろいろ計画しているのでしょうか。頭が上がりません。
さて、このなかよしボードですが、○の有無を書くのは対角線より右の三角形の部分(背景が白くなっているところ)だけで問題ありません。「三郎と五郎は仲が良い」と「五郎と三郎は仲が良い」は同じですので、対角線より右に全ての情報を載せることができます*1。
また先ほどの「どの出場者も、自分より強い出場者で仲が良い人が少なくとも一人いる」という文は、表で見ると「(七郎を除く)どの段にも少なくとも1つの○がある」ということを意味します。白い部分で○がない段はない、ということですね*2。
トーナメントを数えていく
それではここからトーナメントの数を数えていきます。前回の記事に倣って、決勝の左側にあるトーナメントを左予選、決勝の右側にあるトーナメントを右予選と呼ぶことにします。
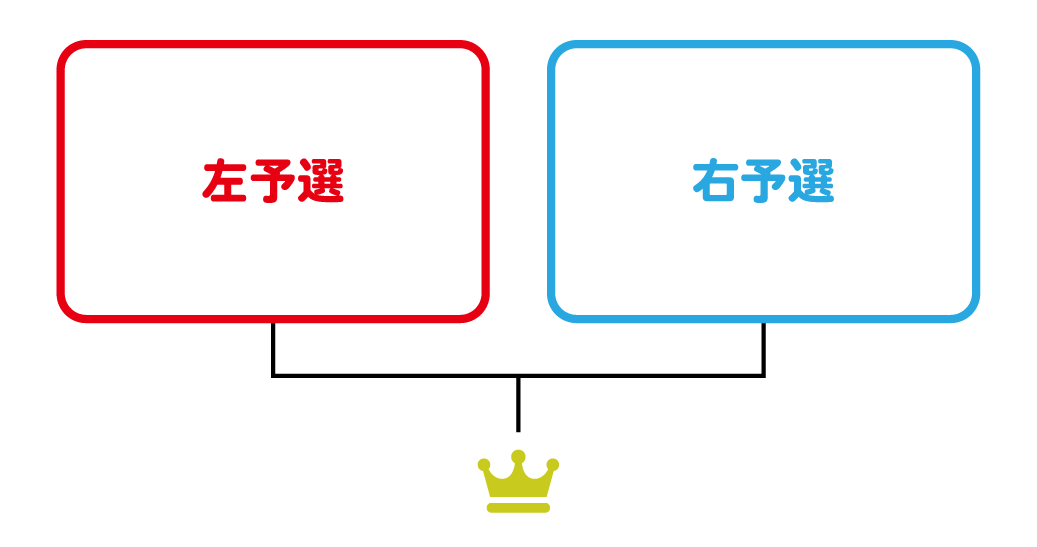
今回の出場者は7人ですから、左予選と右予選の出場者は合わせて7人になります。左予選が2人だったら右予選は5人、左予選が3人だったら右予選は4人です。
このそれぞれの予選の人数の振り分けで場合分けを行ってトーナメントを数え上げて最後にそれを足すことで、知りたかったトーナメントの数を知ることができそうです。
おさらいすると、
- 決勝の左側にあるトーナメントを左予選、右側にあるトーナメントを右予選と呼ぶことにする。
- 左予選を右予選の出場者は合わせて7人である。
- それぞれの予選にどのように人数を振り分けるかで場合分けができる。(2人と5人、3人と4人など)
- 人数の振り分け方それぞれでトーナメントの数を数え上げる。
- 最後に全てのトーナメントの数を足す。
ということですね。
それでは場合分けを行っていきましょう。まずは左予選が1人のときです。
左予選1人、右予選6人のとき
トーナメントとしてはこのようになりますね。

さて、ここで考えていただきたいのが、決勝では誰が対戦することになるのか、です。
まず、左予選を勝ち上がってくるのは誰でしょうか?出場者は一郎だけなので、一郎ですね。
次に、右予選を勝ち上がってくるのは誰でしょうか?二郎〜七郎の出場者がいますが、この中で一番強いのは七郎です。なので、右予選からは七郎が勝ち上がってきます*3。
このことから、左右の予選を1人/6人と振り分けると、決勝戦で一郎と七郎が対戦することになります。
それではこの2人に実際に対戦してもらいましょう。FIGHT!
一郎「………」
七郎「………」
おや?2人とも目を合わせようとすらしませんね。どうしたのでしょうか。
…あっ!!

この2人、仲が悪い!!
せっかく決勝まで来たのに、2人が試合放棄してしまったので大会が成立しませんでした。気まずいですね。
では、なぜこのようなことになってしまったのでしょうか。
理由は簡単です。左右の予選の人数を1人/6人と振り分けてしまったからです。このような予選を行うトーナメントは、どのように作っても決勝で一郎と七郎が当たってしまうのでトーナメントができなくなってしまうのですね。
今回のなかよしボードの様子では、予選を1人/6人と振り分けることは不可能なようです。この振り分け方のトーナメントは0通りでした。かなしいね。
左予選2人、右予選5人のとき
それでは次です。二郎を左予選に入れて、2人/5人という配分で予選を行ってもらいましょう。

同じように、決勝で誰が対戦するのか考えましょう。
左予選では二郎が一番強いので、二郎が勝ち上がります。
右予選では七郎が相変わらず強いので、七郎が勝ち上がります。
それではこの2人に実際に対戦してもら

………。
……0通りです。理由は先ほどと同じです。左右の予選を2人/5人と振り分けると、決勝で二郎と七郎が当たってしまうためですね。みんな仲良くして〜〜
左予選3人、右予選4人のとき
気を取り直して、三郎も左予選に入れて3人/4人という配分にしてみましょう。

決勝進出は誰になるのかは、もうみなさんおわかりですね。
左予選からは三郎、右予選からは七郎が勝ち上がってきます。
…大丈夫かな。ヒヤヒヤしてきました。なかよしボードを確認してみましょう。

この2人、仲が良い!!平和〜〜!!
ということで、左右の予選を3人/4人と振り分けた場合は少なくとも決勝戦は遂行することができるので、トーナメント表を作り上げることができそうです。
実際の数は後ほど数えるとして、残りの場合分けも見ていきましょう。
左予選4~6人のとき(というか全ての場合分け)
残りの場合分けは一気にいきます。
これまでの場合分けの様子を見ていると、決勝戦は一郎〜六郎の誰かと七郎が対戦することがわかります。
左予選はその中で一番強い人が勝ち上がってくるので、1人なら一郎、2人なら二郎、…、6人なら六郎ですね。
いっぽうで右予選は最強の七郎がずっと入っているので、必ず七郎が勝ち上がってきます。
なので七郎と仲が良い人が左予選を勝ち上がってくれないと、そもそも決勝戦を行うことができません。トーナメントを数えるときは、少なくとも決勝戦が行えるようなトーナメントである必要があるわけですね。
では、誰が左予選を勝ち上がればよいのでしょうか?それは表を見れば一目瞭然ですね。七郎と仲が良い人なので、三郎、五郎、六郎です。

ではでは、そのようなトーナメントはどのようなものでしょうか?誰が左予選を勝ち上がるかは左右の予選の人数配分で決まるので、
- 左予選3人(一郎〜三郎) / 右予選4人(四郎〜七郎)
- 左予選5人(一郎〜五郎) / 右予選2人(五郎〜七郎)
- 左予選6人(一郎〜六郎) / 右予選1人(七郎のみ)
の3パターンです。
このそれぞれに対して、左予選と右予選それぞれのトーナメントの総数を求め、それらをかけ合わせ、最後に足すことで、知りたかった総数がわかりそうです。
例えば3人/4人のときは、「一郎〜三郎でのトーナメントの数」と「四郎〜七郎でのトーナメントの数」をそれぞれ求めて、それらをかけ合わせることで3人/4人のトーナメントの総数がわかります。残りの2パターンでも同じことをする、ということです。
どういうこと?と思ったら前回の記事をじっくり読むと良いでしょう。
canaan1008.hatenablog.com
記号の導入
今後トーナメントの数を数えるにあたって、やっぱり記号を使ったほうが計算もしやすいので定義します。
あわてないでください。説明します。まず、僕たちが今回知りたいのは一郎〜七郎が出場者のときのトーナメントの総数なので、です。
の右下にかかれている
と
は、「一郎から七郎まで」という意味です。
そして、これまでの考察から$$
T_{1,7}=T_{1,3}T_{4,7} + T_{1,5}T_{6,7} +T_{1,6}T_{7,7}
$$であることがわかりました。3つあるそれぞれの項が、先ほどの
- 左予選3人(一郎〜三郎で
通り) / 右予選4人(四郎〜七郎で
通り)
- 左予選5人(一郎〜五郎で
通り) / 右予選2人(五郎〜七郎で
通り)
- 左予選6人(一郎〜六郎で
通り) / 右予選1人(七郎のみで
通り)
に対応しています。
もし「どうして左右に分けて、それぞれかけて、最後に足しているの?」と思われた方がいた場合は前回の記事をじっくり読むと良いでしょう(2回目の宣伝)。
canaan1008.hatenablog.com
いったんまとめです。
わかったこと:
ゴリゴリ計算
さて、ここからが見ものですよ!本番です本番!いいですか?
とりあえず丁寧に、(一郎から三郎で作れるトーナメント)から求めてみましょう。
とはどういうことかというと、下図のように一郎から三郎が出場者のときに無事に大会を遂行できるトーナメント表の数を意味します。

そして一郎から三郎のなかよしボードは、もとのなかよしボードの中に既に書いてありました。

では、この3人のトーナメントにおいて左予選と右予選はどのような配分にしましょうか?
左予選と右予選から勝ち上がってきた2人は仲が良い必要があるので…
って、
これまで考えてきたことと同じやないか〜〜〜〜い!!
正確に言うと、「規模は小さくなったけど、考えようとしていることは一緒」ですね。誤解を恐れずに言えば、こういうことを「再帰的(さいきてき)」と言ったりします。いや正確には違うかもしれんけど。
気を取り直して…なかよしボードを見ると、出場者の中で一番強い三郎は一郎とも二郎とも仲が良いので、予選の人数配分は1人/2人と2人/1人の両パターンを網羅できますね。つまり、$$
T_{1,3} = T_{1,1}T_{2,3} + T_{1,2}T_{3,3}
$$となります。出場者が1人のときはトーナメントを組むことができる(誰とも当たらないので仲が悪いペアが当たることがない)ので\begin{eqnarray}
T_{1,1}&=&1 \\
T_{3,3}&=&1
\end{eqnarray}ですね。なのであとは
同様に
さて!諸々求まったのでを計算すると…\begin{eqnarray}
T_{1,3} &=& T_{1,1}T_{2,3} + T_{1,2}T_{3,3} \\
&=& 1 \cdot 1 + 0 \cdot 1 \\
&=& 1
\end{eqnarray}であることがわかりました。やっとがわかりましたね……先は長そうだ。
わかったこと:
さすがに先が長すぎるので、ここから先は適宜説明を加えながら数式の変換をメインにいこうと思います。
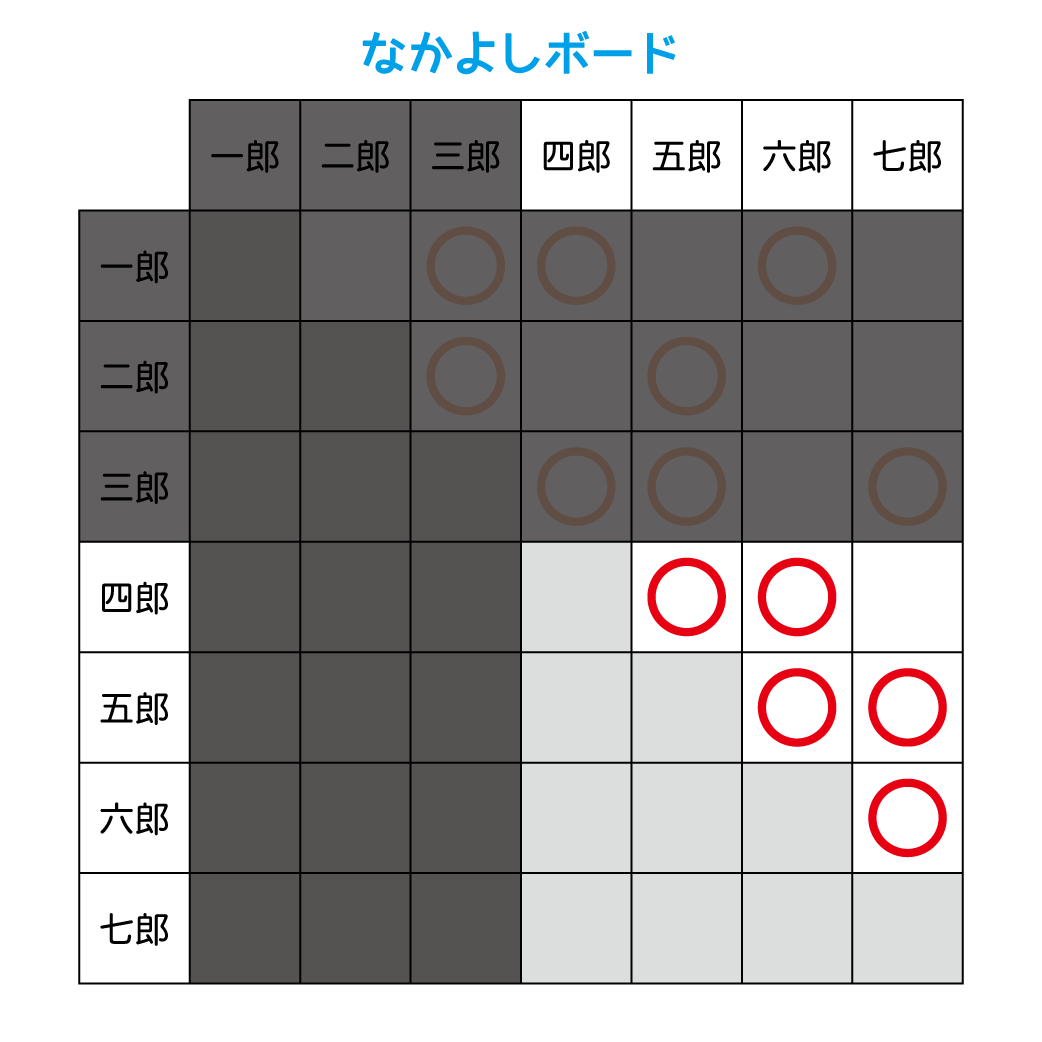
なかよしボードより、四郎と七郎は決勝で会えないため$$
T_{4,7} = T_{4,5}T_{6,7} + T_{4,6}T_{7,7}
$$であり、
T_{4,7} &=& T_{4,5}T_{6,7} + T_{4,6}T_{7,7}\\
&=& 1 \cdot 1 + 2 \cdot 1 \\
&=& 3
\end{eqnarray}となる。
わかったこと:
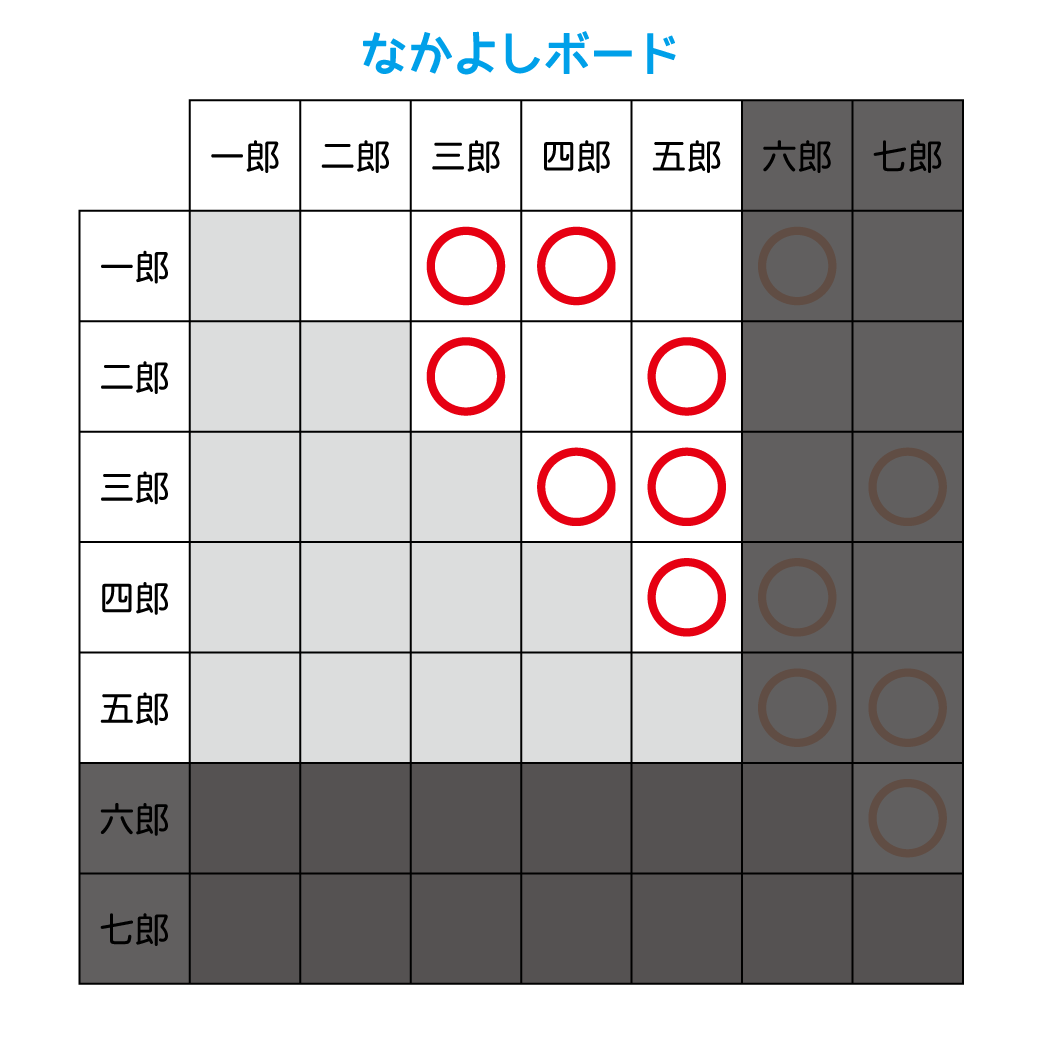
五郎と仲が良い人をみて$$
T_{1,5} = T_{1,2}T_{3,5} + T_{1,3}T_{4,5} + T_{1,4}T_{5,5}
$$わかるところから丁寧に式変形をして…\begin{eqnarray}
T_{1,5} &=& T_{1,2}T_{3,5} + T_{1,3}T_{4,5} + T_{1,4}T_{5,5} \\
&=& 0 \cdot T_{3,5} + 1 \cdot 1 + T_{1,4} \cdot 1 \\
&=& 1 + T_{1,4}
\end{eqnarray}
T_{1,5} &=& 1 + T_{1,4}\\
&=& 1 + T_{1,1}T_{2,4} + T_{1,3}T_{4,4} \\
&=& 1 + 1 \cdot T_{2,4} + 1 \cdot 1 \\
&=& 2 + T_{2,4}
\end{eqnarray}
T_{1,5} &=& 2 + T_{2,4}\\
&=& 2 + T_{2,3}T_{4,4} \\
&=& 2 + 1 \cdot 1\\
&=& 3
\end{eqnarray}となる。
わかったこと:
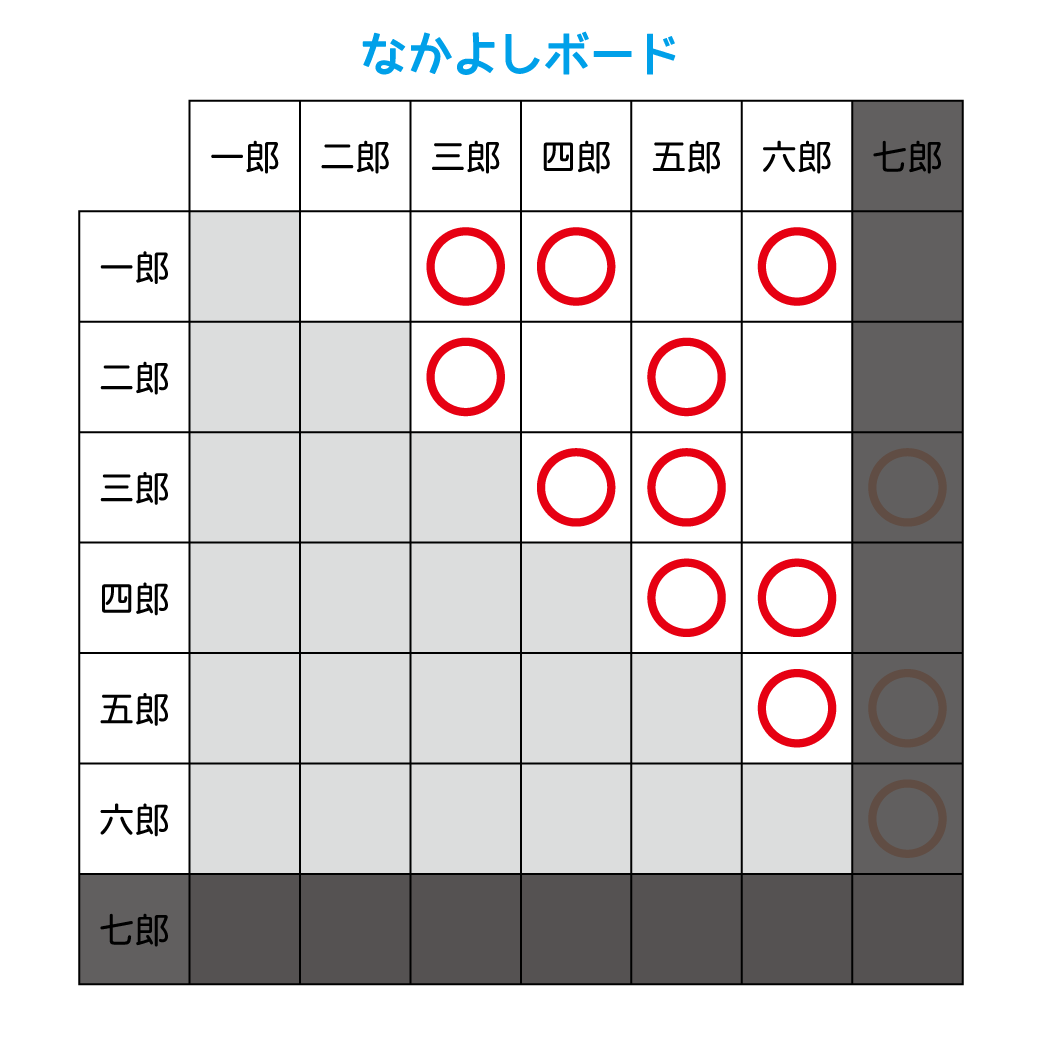
六郎と仲が良い人をみて$$
T_{1,6} = T_{1,1}T_{2,6} + T_{1,4}T_{5,6} + T_{1,5}T_{6,6}
$$わかるところから丁寧に式変形をして…\begin{eqnarray}
T_{1,6} &=& T_{1,1}T_{2,6} + T_{1,4}T_{5,6} + T_{1,5}T_{6,6} \\
&=& 1 \cdot T_{2,6} + 2 \cdot 1 + 3 \cdot 1\\
&=& 5 + T_{2,6}
\end{eqnarray}
 \begin{eqnarray}
\begin{eqnarray}T_{1,6} &=& 5 + T_{2,6} \\
&=& 5 + T_{2,4}T_{5,6} + T_{2,5}T_{6,6} \\
&=& 5 + 1 \cdot 1 + T_{2,5} \cdot 1\\
&=& 6 + T_{2,5}
\end{eqnarray}
T_{1,6} &=& 5 + T_{2,5} \\
&=& 5 + T_{2,2}T_{3,5} + T_{2,3}T_{4,5} + T_{2,4}T_{5,5}\\
&=& 5 + 1 \cdot T_{3,5} + 1 \cdot 1 + 1 \cdot 1\\
&=& 7 + T_{3,5}
\end{eqnarray}
T_{1,6} &=& 7 + T_{3,5}\\
&=& 7 + 2 \\
&=& 9
\end{eqnarray}となる。
T_{1,7} &=& T_{1,3}T_{4,7} + T_{1,5}T_{6,7} +T_{1,6}T_{7,7} \\
&=& 1 \cdot 3 + 3 \cdot 1 + 9 \cdot 1 \\
&=& 15
\end{eqnarray}
なかよしボードが下図のようになっているとき、最後まで大会を遂行できるトーナメント表は15通りある。

まとめ
疲れました。どうしていきなり7人でやってしまったんだ…無茶しやがって…
いろいろややこしくなってしまいましたが、一貫して考えていることは「決勝戦で仲が悪い2人があたらないようにする」ということです。前回のトーナメントを数え上げる記事では左右の予選の人数配分(とそれぞれの予選のトーナメントの数)に着目して数え上げていました。しかし今回のようになかよしボードがあると、予選の人数配分によっては大会を遂行できなくなることがあります。そこに着目し、そのようなパターンは除外して数える必要があったんですね。
「で、多義文の解釈の数え方は結局どうなるの?」「数式で書かれてもわかりづらい」と思うかもしれません。次回の記事ではいよいよ「部分的に黒いポケットに入っている猫が描かれたTシャツを着ている人」の解釈の数え上げをしようと思います。
がんばります。
それでは。