気まずいトーナメントの数え上げ
この記事は前々回の記事の続編です。
canaan1008.hatenablog.com
また、トーナメント表の数え上げ方法をもとに話が進むので、前回の記事を読んでいない方は是非そちらもお読みください。
canaan1008.hatenablog.com
簡単なあらすじ。
「頭が赤い魚を食べた猫」という文章は、文節同士がどうかかり合うかによって5種類の解釈があります。文節同士の全ての組み合わせが可連結かどうか(その2つの文節を繋げて意味が通るかどうか)に着目してトーナメントを作り上げ、無事にトーナメントを作ることができたら意味が通る、という話を行いました。
この記事では、「それぞれの文節同士が可連結かどうか」から「その文章の解釈の総数」を求めることを目標にします。
みなさんも、普段の生活で多義文を見かけることがあると思います。これから書く方法を身につければ、そのような文章を見かけたときに「この文章は○通りの解釈ができてしまうのでよくありませんね」とドヤ顔で言うことができます。たのしみですね
ちなみにこのあと例え話に移っていきますが、今回は多義文の話に戻ってきません。ゆるしてね
次の記事でその点は書きたい。
トーナメントの数え上げ
この記事は前回の記事の続編…にしようと思ったのですが、予備知識について書いていたら1.5記事ぶんくらいになったので単体の記事にしました。
canaan1008.hatenablog.com
今後の方針としては、↑の記事で扱ったような多義文の解釈の数え上げについて触れる予定です。
要するに、可連結かどうかの制限付きなトーナメントの数え上げをしたいわけです。
ですが、この数え上げをするにはそもそも可連結かどうかの制限がないトーナメントの数え上げについて理解する必要がありました。そりゃそうだよね
ということで、一旦多義文のことは忘れてトーナメントの数え上げについて考えていきます。
続きを読む部分的に黒い猫と赤い魚を食べた猫(多義文の話)
この記事は 数学デー Advent Calendar 2019 - Adventar の8日目の記事です。
あらすじ
9月。
東京で仕事を見つけた僕は、上京にあたって密かに楽しみにしているものがあった。
そう。数学デーである。
上京して最初の水曜日。仕事を少し早めに離脱した僕は、わくわくしながら神田駅へ向かった。
どんな話が広がっているんだろう。仲良くなれるかな。どれくらい知っている人がいるのかな。
いろいろな思いを胸に秘めながら、株式会社ソノリテのインターホンを押した。
そこに見えたのは、大きなホワイトボードシートに乱れ書きされた数式やグラフのようなものと、それを取り囲む人たち。
Twitterで見たことある光景そのままが目の前に広がっていた。
知っている方に軽く挨拶を済ませ、どんな話題が広がっていたのかを観察する。
「今は、頭が赤い魚を食べた猫の話をしていたんですよ」
僕「ああ、聞いたことあります。いろんな意味にとれちゃうってやつ」
「そうですね」
「ん…？」
皆の視線が僕が来ていたTシャツに集まった。
「猫のTシャツだ」
「ポケットに入っている猫ですね」「部分的に黒い猫だ」「猫が描かれたTシャツを着ている人…」
僕「え、え、」
僕の胸元を見ながら議論が突然白熱し、数分後にはホワイトボードにこのような文が書かれていた。
部分的に黒いポケットに入っている猫が描かれたTシャツを着ている人
数学デーってスゴイ、実際に行ってみてそう思った。
本日は、頭が赤い魚を食べた猫の解釈を考えいるときに部分的に黒いポケットに入っている猫が描かれたTシャツを来ている人がいらっしゃったので、その解釈を考えました。（キグロ）#数学デー #ソノリテ数学デー pic.twitter.com/VlCGgrHz4K
— 「数学デー」公式 (@sugaku_day) 2019年9月11日
糸掛けに出てくる花の秘密を研究していたら想像以上に美しかった話
先日、糸掛けを趣味にしている知り合いの方がFacebookにこのような作品を上げていました。
『謎が解けた⁉️』
誰かに『渦を作ると花が出来上がるのは何でやねん』と突っ込まれた事があった。
答えが解らんと、その時は誤魔化した(笑)
で。多分、約数が関連してるのかと感じたのは、ついさっき。この作品。
使ってる数字が『１』『２』『３』『16』『24』『48』なのでこれが糸の掛け方と関連してるんじゃないかと思われる、多分。
難しい事は、他の得意な方々に任せよう。
僕「研究するしかねえな？」
ということで、何故このような花柄ができるのかを数学的に研究することにしました。
続きを読む【レビュー】小野田博一 著『数学難問BEST100』『数学〈超絶〉難問』『数学〈超・超絶〉難問』を読んで
みなさんこんにちは。カナンです。
小野田博一さんが書いた数学の問題集を3年ほどかけてずっと解き続けていたのですが、やっと完走したのでレビューをしたいと思います。
今回レビューするのは以下の3冊です。
- 数学難問BEST100
- 数学〈超絶〉難問
- 数学〈超・超絶〉難問
- 作者: 小野田博一
- 出版社/メーカー: PHP研究所
- 発売日: 2015/02/27
- メディア: 単行本（ソフトカバー）
- この商品を含むブログを見る
- 作者: 小野田博一
- 出版社/メーカー: 日本実業出版社
- 発売日: 2014/05/22
- メディア: 単行本
- この商品を含むブログ (1件) を見る
- 作者: 小野田博一
- 出版社/メーカー: 日本実業出版社
- 発売日: 2017/08/10
- メディア: 単行本（ソフトカバー）
- この商品を含むブログを見る
それぞれの問題集の難易度の違い等には触れませんが、3冊全体を通して思ったことなどを書きます。
解いてみたいと思った方は、上記の順番に難しくなっている(と思う)ので興味のあるものから手をつけてみてください。
また、問題や解答の内容を引用している部分があります。もしかしたらネタバレに繋がる可能性もあるため、解くかもしれない方はご注意ください。
続きを読む「謎解き数学」のヒント＆解答＆解説
みなさんこんにちは。カナンです。
以前公開した「謎解き数学」に載せた謎およびカナンの挑戦状の解説をしたいと思います。
壮大なネタバレを含みますので、まだ解いていない方は是非ご自分の手で解いてみてからこの記事を読んでください。
追記：カナンの挑戦状のCの問題ですが、不備(別解)がありました。失礼いたしました。
答えは「４文字の数学用語」になります。
よろしくお願いいたします。
答えは「４文字の数学用語」になります。
よろしくお願いいたします。
まだ解けていない人のために、ヒントをいくつか差し上げたいと思います。
ヒント
$T=1, E=7, A=9$です。
これだけでは解けない問題がほとんどです。まずはプレゼン中に出題した謎を解いてみましょう。
このような○がついた矢印をどこかで見かけたはずです。
横向きにして解き直してみましょう。
このような赤線を４箇所、スライドのどこかで見かけませんでしたか？
緑、赤、黄、青の４つの色で塗り分けられた絵を見た覚えはないでしょうか？
もしくは自分の手で塗った覚えは…
答えはカタカナ３文字になります。
２文字目は赤と青の枠がくっついて一つのカタカナになります。
ダジャレです。
ドミノ倒しに例えられることが多い証明方法です。
もう一度このスライドを最初から見てみましょう。
「通らない文字」とありますが、そもそも文字の上を通った覚えはありませんか？
ひらがなの上を通過する問題がどこかにあるはずです。
数字に変換して、計算して、アルファベットに変換しましょう。
４つの矢印はそれぞれ言葉を変換するようです。
逆向きの矢印があることに注意しましょう。
４つの漢字をそれぞれ置き換えているようですね。
置き換えることで別の問題に変わるようです。
解答欄に文字を入れ、赤線の部分を読んでみましょう。
Fの問題はあらかじめ黒で濁点が書いてあるため、赤線の部分を読む時は濁点は外して読めばOKです。
「たいとるのかしらもじ」というのはメッセージとしては不自然ですね。では「タイトルの頭文字」を読んだらメッセージが浮かび上がるとしたら…？
もう一度このスライドを広く見渡してみましょう。
三次関数のグラフの対称性を初めて調べた話
グラフには直線や放物線などがあるのはご存知だと思います。
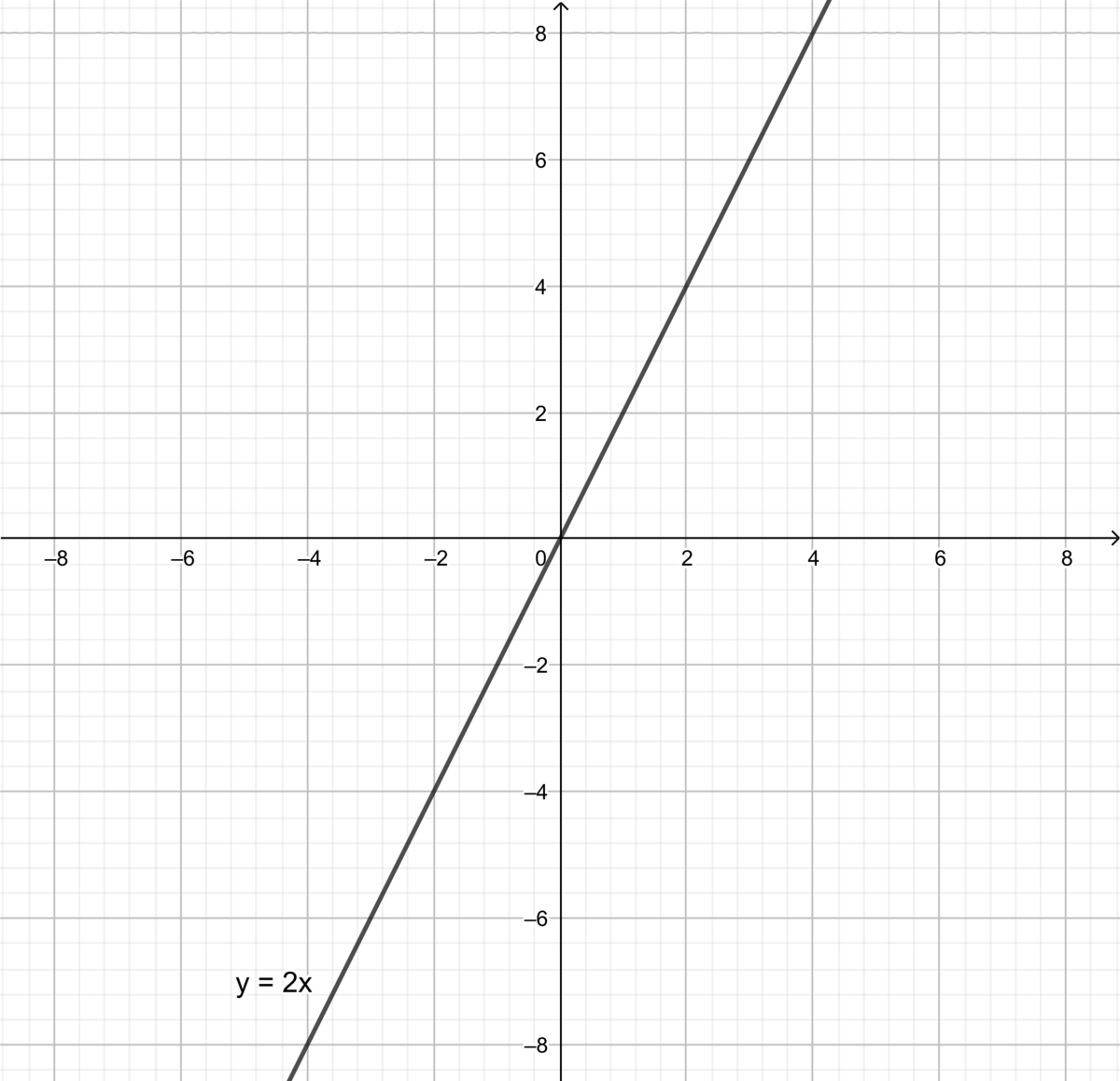
直線は例えば$y=2x$みたいな一次式で表されるものですし、放物線は$y=x^2+x-1$のような二次式で表されるものがそうです。
$y=2x$のグラフ
$y=x^2+x-1$のグラフ
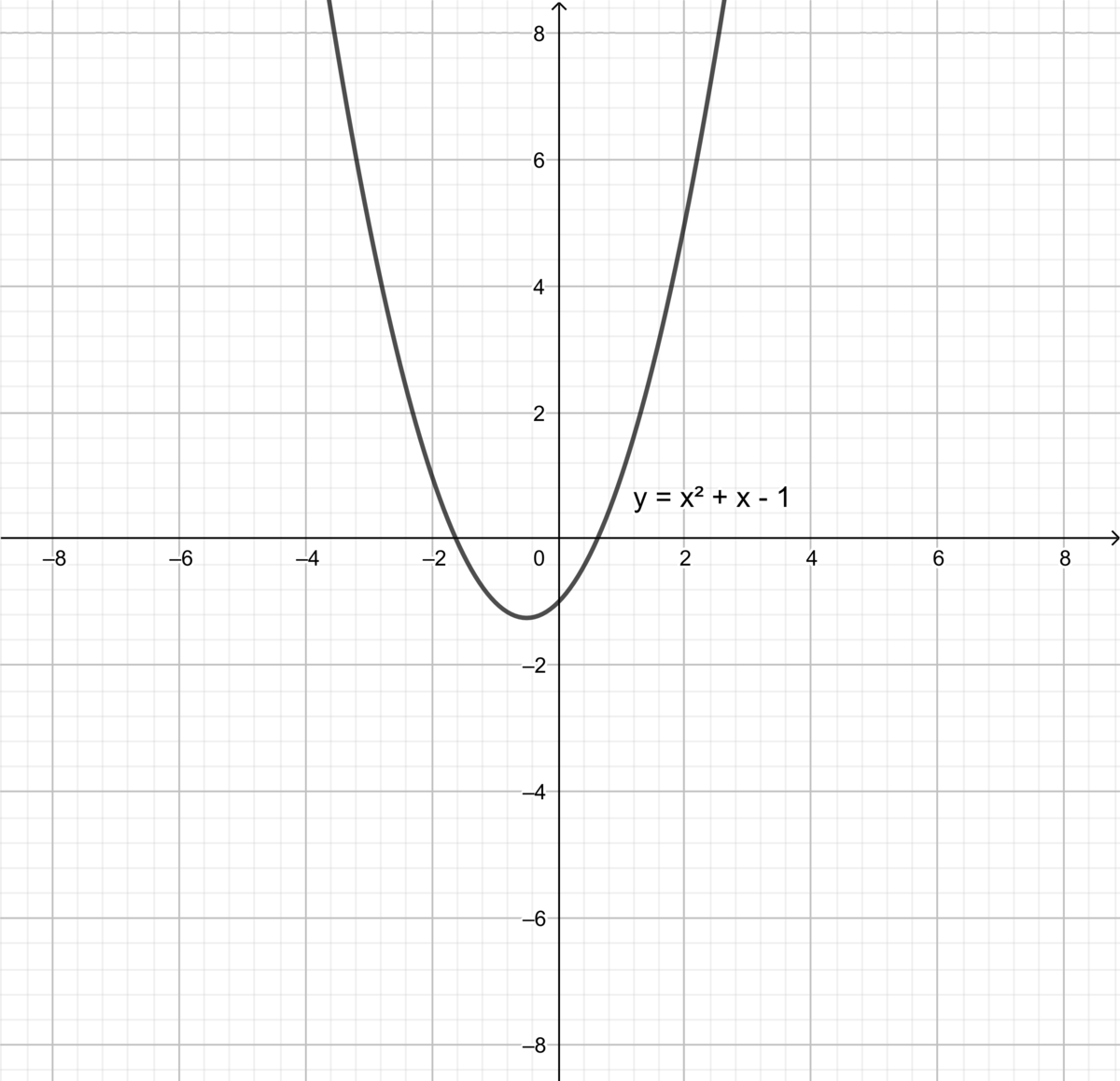
どちらのグラフもとても高い対称性があることがひと目でわかります。
一次関数の$y=2x$は直線上の点について点対称ですし、二次関数の$y=x^2+x-1$は軸について線対称ですね。
ここで気になるのが、三次関数の対称性です。
なんとなく「点対称っぽいな〜〜」とは感じていたのですが、自分の手で確かめたことが無かったのであやふやだったんですよね。
ということで調べてみました。